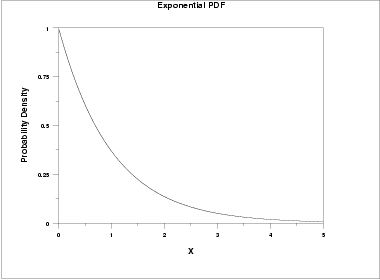
Exponential distribution graph
Accordingly Section 3 is devoted to a discussion of exponential families focusing on the mathematical links to convex analysis and thus anticipating our development of variational meth-ods. Small values have relatively high probabilities which consistently decline as data values increase.
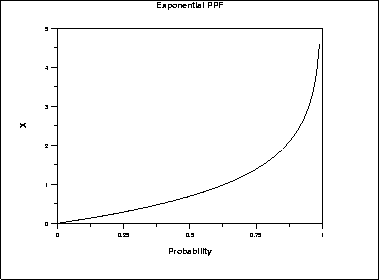
1 3 6 6 7 Exponential Distribution
A variable X is said to possess an exponential distribution when.
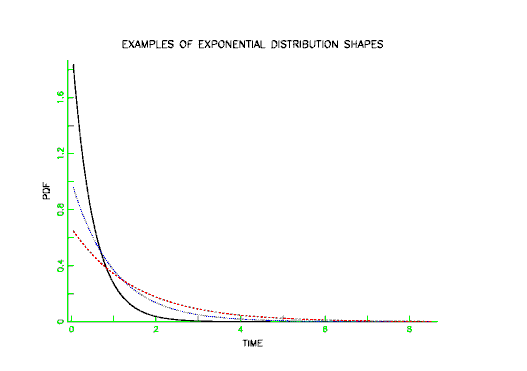
. The exponential distribution graph is a graph of the probability density function which shows the distribution of distance or time taken between events. The graph is smooth. With β 1 the usual exponential function is recoveredWith a stretching exponent β between 0 and 1 the graph of log f versus t is characteristically stretched hence the name of the functionThe compressed exponential.
To start Ill illustrate how changing alpha affects your results. Where λ stands for rate and always has value greater than zero. Then the maximum value out of.
The value of a is 005. The two terms used in the exponential distribution graph is lambda λand x. Concretely let be the probability distribution of and its cumulative distribution.
Here lambda represents the events per unit time and x represents the time. Gumbel has shown that the maximum value or last order statistic in a sample of random variables following an exponential distribution minus the natural logarithm of the sample size approaches the Gumbel distribution as the sample size increases. Note that the decay rate.
Free exponential equation calculator - solve exponential equations step-by-step. The properties of the exponential function and its graph when the base is between 0 and 1 are given. Example of Simple Exponential Smoothing.
To compute the value of y we will use the EXP function in Excel so that the exponential formula will be. Then we will print the converted number. The exponential distribution aka negative exponential distribution explained with examples solved exercises and detailed proofs of important results.
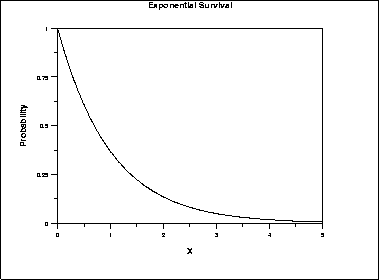
Chemical Reactions Chemical Properties. The first graph red line is the probability density function of an exponential random variable with rate parameter. Exponential distribution is used for survival analysis for example life of an air conditioner expected life of a machineand length of time between metro arrivals.
First we will declare an exponential number and save it in a variable. The exponential distribution is a right-skewed continuous probability distribution that models variables in which small values occur more frequently than higher values. In the time series plots below I use an alpha of 02 in the top graph and 08 in the lower chart.
Is obtained by inserting a fractional power law into the exponential functionIn most applications it is meaningful only for arguments t between 0 and. The line passes through the point 01. The graph below displays this distribution.
Then we will use the float function to convert it to float datatype. The number of infected people increases gradually at a fast rate and the growth is undoubtedly exponential in nature. View interactive graph Examples.
The graph of exponential distribution is shown. For instance a saving account that is applied with an annual compound interest tends to give exponential returns to the account holder. For example in physics it is often used to measure radioactive decay in engineering it is used to measure the time associated with receiving a defective part on an assembly line and in finance it is often used to measure the likelihood of.
A EXP-2x Applying the exponential formula with the relative reference Relative Reference In Excel relative references are a type of cell reference that changes when the same formula is copied to different cells or worksheets. The exponential Weighted Mean method is used to calculate EMA which takes a decay constant as a parameter. As the plot of EMA values is little smoothened when compared to Original Stock values indicates the nature of Exponential Moving Averages.
The graph is continuous. Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution. The graph increases without bound as x approaches positive infinity.
In particular the principal object of interest in our exposition is a certain conjugate dual relation associated with exponential. For this example well use simple exponential smoothing to model the demand for a product. One of the best examples of exponential growth can be found in the finance domain.
Exponential Function Graph y2-x The graph of function y2-x is shown above. A continuous random variable X is said to have an Exponentialλ distribution if it has probability density function f Xxλ ˆ λeλx for x0 0 for x 0 where λ0 is called the rate of the distribution. In the study of continuous-time stochastic processes the exponential distribution is usually used.
Floatx The float method is used to return a floating-point number from a number or a string. The exponential distribution is a continuous distribution that is commonly used to measure the expected time for an event to occur.

Negative Exponential Distribution An Overview Sciencedirect Topics
5 4 The Exponential Distribution Statistics Libretexts
1 3 6 6 7 Exponential Distribution

How To Plot An Exponential Distribution In R Statology

Exponential Distribution Chart Calculator High Accuracy Calculation

8 1 6 1 Exponential

Exponential Distribution An Overview Sciencedirect Topics
5 4 The Exponential Distribution Statistics Libretexts
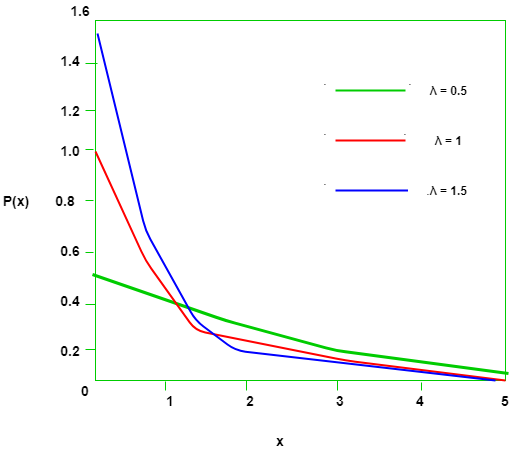
Mathematics Probability Distributions Set 2 Exponential Distribution Geeksforgeeks
1 3 6 6 7 Exponential Distribution

Exponential Distribution In R Dexp Pexp Qexp And Rexp Functions
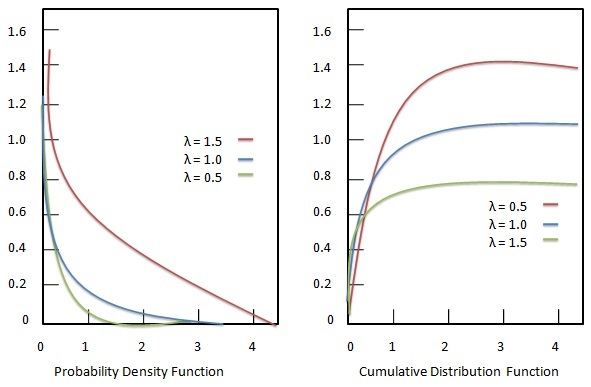
Statistics Exponential Distribution

10 Exponential Distribution Examples In Real Life Studiousguy
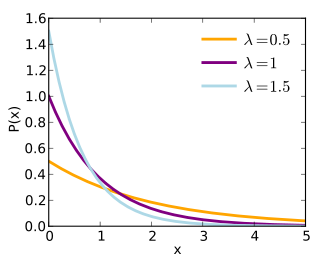
Rate Parameter Statistics How To

How To Plot An Exponential Distribution In R Statology

Exponential Distribution Uses Parameters Examples Statistics By Jim

Exponential Distribution Uses Parameters Examples Statistics By Jim